|
In communication systems, estimating the carrier frequency offset (CFO) is crucial to achieve reliable signal demodulation and decoding at the receiver. This is especially true when dealing with complex I and Q signals, where variations in the carrier frequency can introduce distortions and errors in the received data. Fortunately, there are methods available to apply estimated CFO to complex I and Q signals, ensuring accurate reception and subsequent processing.
One commonly used technique for CFO estimation is based on pilot symbols, which are known and periodically inserted in the transmitted signal. By measuring the phase differences between the received pilot symbols, the CFO can be estimated and compensated for. This method works well for simple modulation schemes, but for complex signals, additional steps need to be taken.
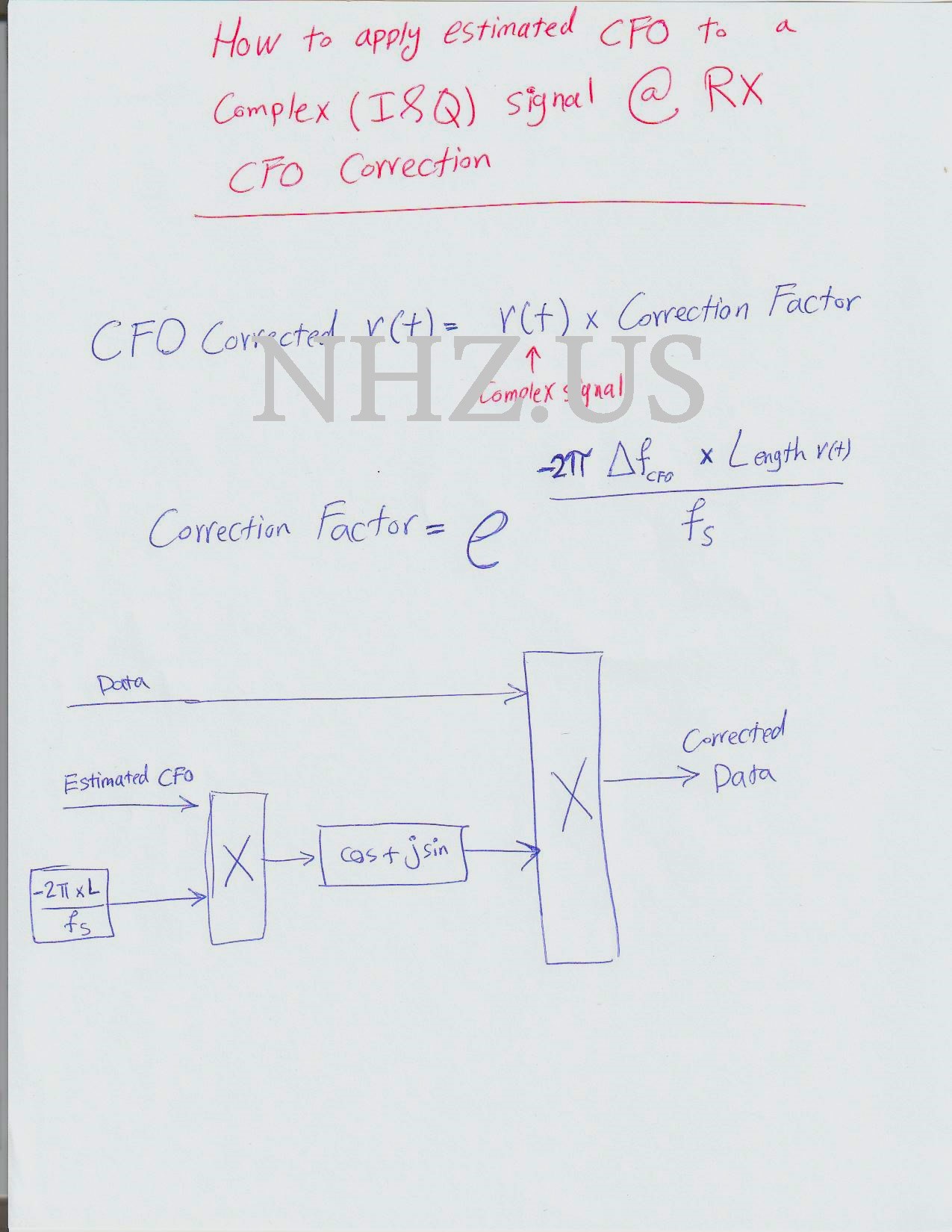
To apply estimated CFO to a complex I and Q signal, the received signal is first split into its in-phase (I) and quadrature (Q) components. This can be achieved using a digital signal processing algorithm or specialized hardware. The CFO estimation is then performed separately on the I and Q components.
Once the CFO is estimated for both I and Q components, it needs to be compensated for by applying an appropriate frequency correction. This correction is typically achieved by multiplying the I and Q signals with complex exponential terms that represent the estimated CFO. The corrected I and Q signals are then combined to reconstruct the complex signal.
After applying the estimated CFO, the demodulation and decoding processes can proceed as usual. However, it is important to note that the CFO estimation and compensation steps need to be repeated periodically, as the carrier frequency offset may change over time due to various factors such as Doppler shifts or local oscillator instabilities.
In conclusion, applying estimated CFO to a complex I and Q signal at the receiver involves splitting the received signal into I and Q components, estimating the CFO separately for each component, and compensating for the estimated CFO by applying frequency corrections. This process ensures accurate reception and processing of complex signals, enabling reliable communication in challenging environments.
Q: What does CFO stand for in the context of a receiver?
A: CFO stands for Carrier Frequency Offset.
Q: Why is it important to estimate the CFO in a receiver?
A: Estimating the CFO helps correct the carrier frequency offset caused by imperfections in the transmitter and receiver clocks.
Q: What is a complex I and Q signal?
A: A complex I and Q signal, also known as a baseband signal, consists of an in-phase component (I) and a quadrature component (Q) that together represent the modulated information.
Q: How can the CFO be estimated at the receiver?
A: The CFO can be estimated by using pilot signals or known training sequences.
Q: What is the purpose of applying the estimated CFO to the complex I and Q signal?
A: Applying the estimated CFO helps compensate for the carrier frequency offset and correctly demodulate the received signal.
Q: What are the typical methods used to apply the estimated CFO?
A: Some common methods include frequency shift correction, phase rotation correction, or complex multiplication with a corrective carrier signal.
Q: What are the potential consequences of not applying the estimated CFO to the complex I and Q signal?
A: Failing to account for the CFO may result in symbol misalignment, loss of data, or degraded signal quality.
Q: Can the CFO estimation and correction be performed in real-time?
A: Yes, with efficient algorithms and hardware processing, it is possible to estimate and correct the CFO in real-time.
Q: Are there any challenges or limitations in applying estimated CFO to a complex I and Q signal?
A: Yes, challenges may arise due to frequency drifts, noise, multipath fading, or non-ideal synchronization of transmitter and receiver clocks.
Q: How does the accuracy of the CFO estimation impact signal reception?
A: The accuracy of CFO estimation directly affects the demodulation accuracy, and thus impacts the bit error rate (BER) of the received signal.
| Question |
Answer |
| What does CFO stand for in the context of a receiver? |
CFO stands for Carrier Frequency Offset. |
| Why is it important to estimate the CFO in a receiver? |
Estimating the CFO helps correct the carrier frequency offset caused by imperfections in the transmitter and receiver clocks. |
| What is a complex I and Q signal? |
A complex I and Q signal, also known as a baseband signal, consists of an in-phase component (I) and a quadrature component (Q) that together represent the modulated information. |
| How can the CFO be estimated at the receiver? |
The CFO can be estimated by using pilot signals or known training sequences. |
| What is the purpose of applying the estimated CFO to the complex I and Q signal? |
Applying the estimated CFO helps compensate for the carrier frequency offset and correctly demodulate the received signal. |
| What are the typical methods used to apply the estimated CFO? |
Some common methods include frequency shift correction, phase rotation correction, or complex multiplication with a corrective carrier signal. |
| What are the potential consequences of not applying the estimated CFO to the complex I and Q signal? |
Failing to account for the CFO may result in symbol misalignment, loss of data, or degraded signal quality. |
| Can the CFO estimation and correction be performed in real-time? |
Yes, with efficient algorithms and hardware processing, it is possible to estimate and correct the CFO in real-time. |
| Are there any challenges or limitations in applying estimated CFO to a complex I and Q signal? |
Yes, challenges may arise due to frequency drifts, noise, multipath fading, or non-ideal synchronization of transmitter and receiver clocks. |
| How does the accuracy of the CFO estimation impact signal reception? |
The accuracy of CFO estimation directly affects the demodulation accuracy, and thus impacts the bit error rate (BER) of the received signal. |
```
Step 1:
Initially, obtain the received complex I and Q signals from the receiver. These signals represent the in-phase and quadrature components of the received signal.
|
Step 2:
Calculate the instantaneous frequency offset between the received signal and the expected carrier frequency. This can be done using a phase-locked loop (PLL) or other frequency estimation techniques.
|
Step 3:
Apply the estimated frequency offset to the complex I and Q signals. This involves multiplying the I and Q components by a complex sinusoid with the opposite sign of the estimated frequency offset.
|
Step 4:
Implement a low-pass filter to suppress high-frequency noise and interference present in the signal after applying the frequency offset. The filter should have an appropriate cutoff frequency to preserve the desired signal components while removing unwanted noise.
|
Step 5:
Perform carrier recovery by employing a method such as a phase-locked loop (PLL) or a Costas loop. This aims to estimate and correct the phase offset introduced by the frequency offset applied in step 3.
|
Step 6:
Process the complex I and Q signals using the recovered carrier phase. This entails rotating the complex I and Q signals by the negative of the estimated carrier phase to align them with the original signal.
|
Step 7:
Extract the desired information from the complex I and Q signals after carrier recovery. This may involve demodulating the signal, performing further processing, or decoding the received data, depending on the specific application.
|
Step 8:
Finally, analyze and use the extracted information as required for your particular application.
|

|
