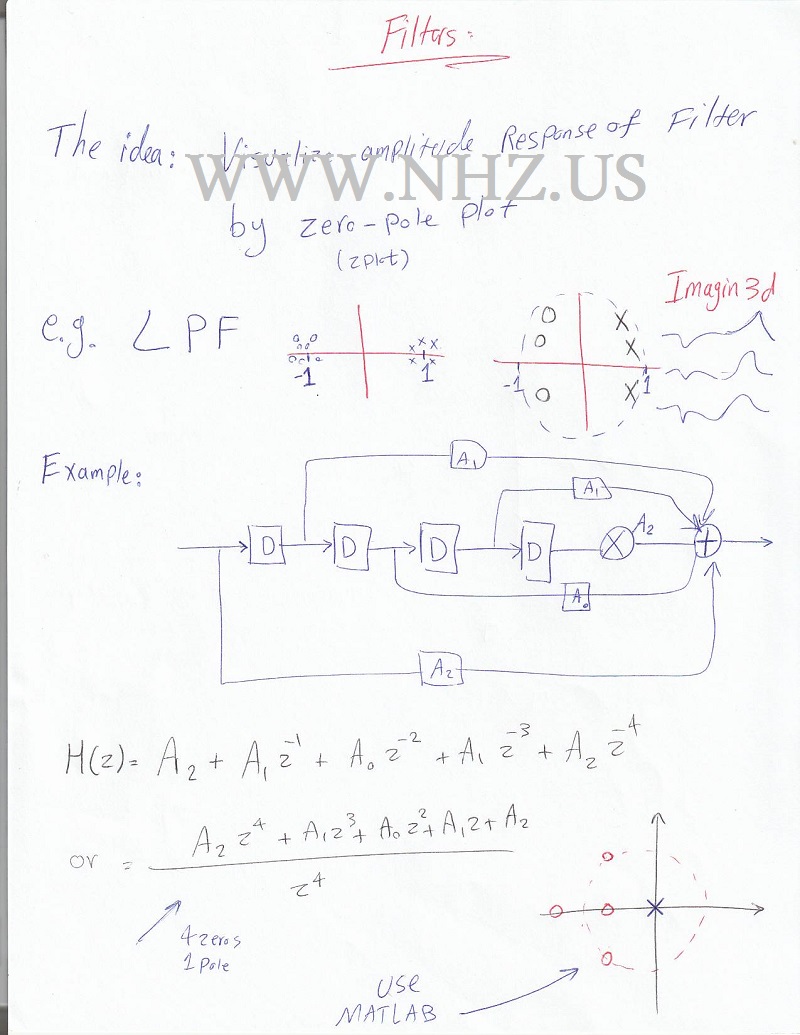
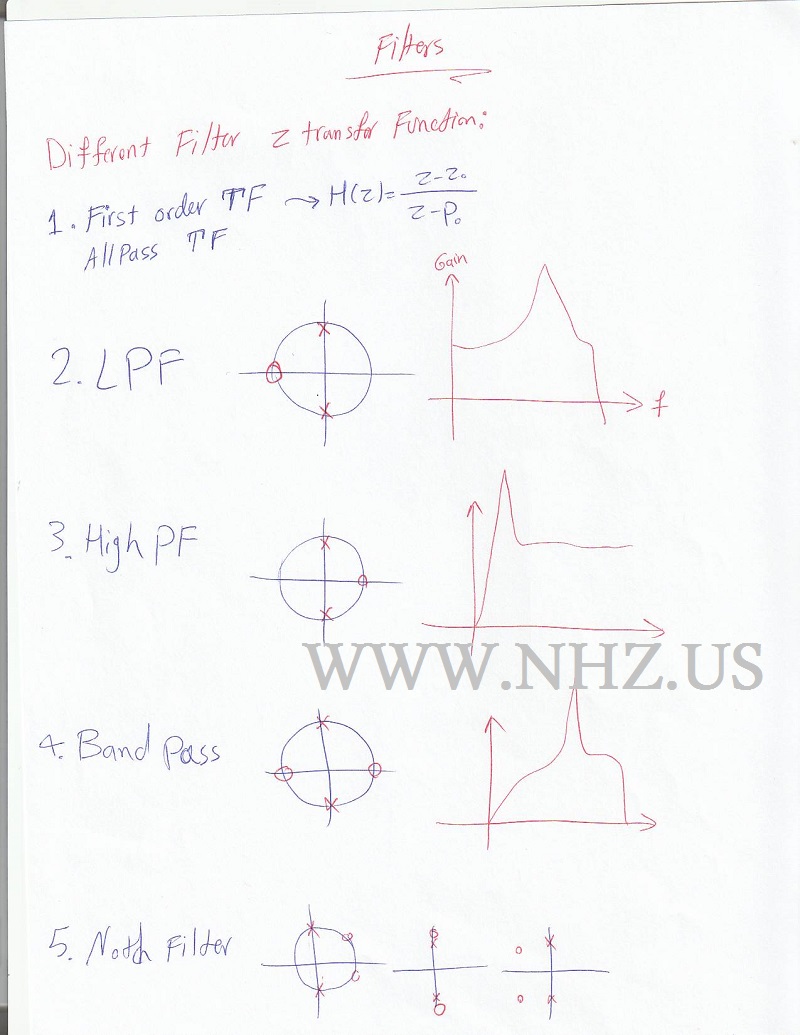
Z Transform and Its Relationship to Filter Design

The Z Transform is a cornerstone of digital signal processing, particularly in the realm of filter design. It provides a method for analyzing and designing systems by transforming discrete-time signals into a complex frequency domain representation. This transformation is crucial for understanding and manipulating signals in various applications, including communications, audio processing, and control systems.

Understanding the Z Transform

To comprehend the Z Transform, let's start with its definition. The Z Transform of a discrete-time signal \( x[n] \) is a complex function defined as:

X(z) = Σ (from n=-∞ to ∞) x[n] z^-n

Here, \( z \) is a complex number represented as \( z = re^{jω} \), where \( r \) is the magnitude and \( ω \) is the phase angle. This transformation shifts the signal from the time domain to the z-domain, where it can be analyzed more conveniently.

The Region of Convergence (ROC)

The Region of Convergence (ROC) is an essential concept in the Z Transform. It is the range of values of \( z \) for which the Z Transform converges to a finite value. The ROC is critical because it determines the stability and causality of the system.

For example, consider the sequence \( x[n] = a^n \). The Z Transform is:

X(z) = 1 / (1 - az^-1)

The ROC for this transform is \( |z| > |a| \).

Relationship to Filter Design

In digital signal processing, filters are used to remove unwanted components from a signal or to enhance specific aspects of it. The Z Transform is integral to filter design because it enables the analysis of a filter's frequency response and stability.

Types of Filters

There are several types of filters, each serving a different purpose:

Low-pass filters: Allow low frequencies to pass through and attenuate high frequencies.
High-pass filters: Allow high frequencies to pass through and attenuate low frequencies.
Band-pass filters: Allow a specific range of frequencies to pass through.
Band-stop filters: Attenuate a specific range of frequencies.

Designing Filters Using the Z Transform

Filter design involves determining the coefficients that define the filter's response. The Z Transform plays a crucial role in this process. Here's a step-by-step approach to designing a simple digital filter:

Step 1: Define the Desired Frequency Response

First, we define the desired frequency response \( H(z) \). For instance, for a simple low-pass filter, we might choose:

H(z) = 1 / (1 - 0.5z^-1)

Step 2: Determine the Filter Coefficients

The next step is to determine the filter coefficients that will achieve the desired response. In this case, the coefficients are \( 1 \) and \( 0.5 \).

Step 3: Implement the Filter

Finally, we implement the filter using these coefficients. In practice, this often involves programming the filter into a digital signal processing system.

Advanced Filter Design: Example

Let's consider a more advanced example: designing a band-pass filter. Suppose we want a filter that allows frequencies between \( f1 \) and \( f2 \) to pass through while attenuating all other frequencies. We can start by defining the desired frequency response:

H(z) = (z - z1)(z - z2) / (z - p1)(z - p2)

where \( z1 \) and \( z2 \) are the zeros of the filter (frequencies we want to pass) and \( p1 \) and \( p2 \) are the poles (frequencies we want to attenuate).

Applications of the Z Transform in Filter Design

The Z Transform is widely used in various applications, including:

Audio Processing: Filters are used to enhance audio signals, remove noise, and apply effects.
Communications: Filters help in extracting desired signals from a noisy environment.
Control Systems: Filters are used to ensure stability and desired response in control systems.

Question and Answer

Q: What is the Z Transform?

A: The Z Transform is a mathematical tool used to convert discrete-time signals into a complex frequency domain representation.

Q: Why is the Z Transform important in filter design?

A: It allows us to analyze and design filters by working with signals in the frequency domain, making it easier to understand the filter's behavior.

Q: What are the main types of filters?

A: The main types are low-pass, high-pass, band-pass, and band-stop filters.

Q: How does the Z Transform help in designing a filter?

A: The Z Transform helps in determining the filter's coefficients and analyzing its frequency response, which are crucial steps in filter design.

Conclusion

The Z Transform is a powerful and essential tool in digital signal processing, particularly in the design of filters. By transforming signals into the frequency domain, it simplifies the analysis and design process, allowing for precise control over the filter's behavior. Whether you're working on audio processing, communications, or control systems, understanding the Z Transform and its relationship to filter design is crucial.

Examples

Example 1: Low-pass Filter

H(z) = 1 / (1 - 0.5z^-1)

This filter allows low frequencies to pass and attenuates high frequencies.

Example 2: High-pass Filter

H(z) = (1 - 0.5z^-1)

This filter allows high frequencies to pass and attenuates low frequencies.

Example 3: Band-pass Filter

H(z) = (z - 0.5)(z - 0.7) / (z - 0.2)(z - 0.9)

This filter allows frequencies between 0.5 and 0.7 to pass and attenuates others.